Dach do samodzielnego montażu
Współcześnie w budownictwie indywidualnym domów jednorodzinnych spotyka się wszystkie rodzaje więźb dachowych tj. krokwiowe, jętkowe, płatwiowe ze stolcem pojedynczym, płatwiowe ze stolcem podwójnym z jętkami lub kleszczami, płatwiowe z ustrojem kozłowym lub wieszarowym.
Analizując te rodzaje ustrojów więźb możemy stwierdzić, że są one pochodną więźby o ustroju płatwiowym ze stolcem podwójnym z kleszczami.
Ustrój takiej więźby przedstawia rys. 1. Ponieważ dach jest wizytówką budynku ważne jest jego wykonanie zgodnie z dokumentacją, tak w odniesieniu do murarza, który przygotowuje bazę więźby, jak i do cieśli. Cieśla musi go wykonać zgodnie z narzuconymi parametrami dachu tj. pochyleniem dachu wyrażonym w stopniach lub w procentach oraz z wymiarami zewnętrznymi. Źródłami informacji o parametrach więźby są w dokumentacji rzuty dachu oraz przekroje. Niestety mimo coraz powszechniej stosowanych w projektowaniu programów komputerowych, dokumentacja dachu przedstawia wiele do życzenia. Najczęściej jest to dokumentacja konstrukcyjna, zbyt mało przystosowana do wykonawstwa. Uważam, że jest to wynik małego kontaktu projektanta z praktyką.
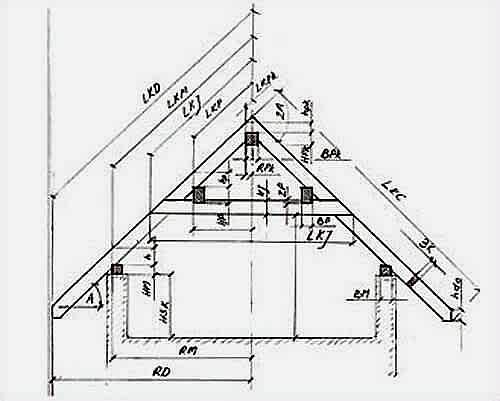
W wyniku wieloletniego doświadczenia opracowałem metodę wykonania więźby dachowej, którą nazwałem „więźbą do samodzielnego montażu”. Metoda ta różni się od tradycyjnej tym, że więźba może być wykonywana np. w zakładzie stolarskim lub ciesielskim daleko od budowy. Tradycja zna taki sposób wyznaczania więźby tzw. odwiązywanie, ale dotyczy to tylko więźb dwupołaciowych. Moja metoda obejmuje więźby wielopołaciowe i polega na wyznaczeniu kształtu dachu matematycznie i wykonaniu jego elementów w sposób stolarski. Punktem wyjścia do więźby jest dokładny obmiar murów budynku oraz przekrój więźby z dokumentacji. Na rysunku 2 przedstawiam wszystkie istotne wymiary potrzebne dla wykonawcy.
Stosując zależności geometryczne można określić wymiary elementów dachu. I tak:
LKPK = RPK/cos A
LKP = RP/cos A
LKM = RM/cos A
LKD = RD/cos A
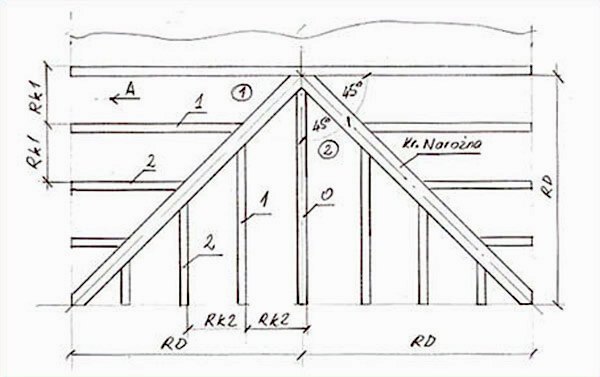
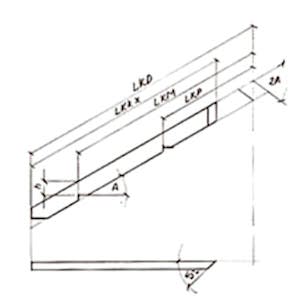
Według nich następnie wykonuję elementy, stosując np. do wyznaczania wrębów na krokwi, skonstruowany przez siebie kątomierz nastawny oraz kątownik stały. Wręby zgodnie z rys.2 rysuję na ułożonej na boku krokwi, bazując na wcześniej narysowanych na grzbiecie krokwi liniach zgodnych z wymiarami LKPK, LKP, LKM, LKD. Do wykonania zaciosów kalenicy używam drugiego kątomierza nastawnego. Aby wręby i zaciosy były dokładnie wykonane, wykonuję je pilarką tarczową oraz płatnicą ręczną. W przypadku więźb wielopołaciowych zagadnienie sprowadza się do podzielenia dachu na pary połaci. Najprostszym typem takiej więźby jest tzw. „koperta” o połaciach nachylonych pod kątami A1 = A2 – rys. 3.
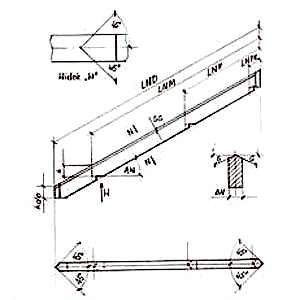
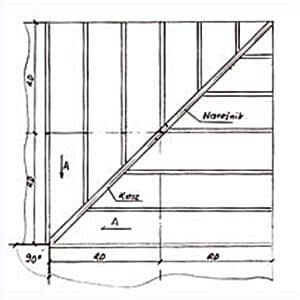
W tej więźbie wykonawcom największą trudność sprawia krokiew narożna, ponieważ jest nachylona pod innym niż połacie kątem – AN. W tym przypadku na pomoc przychodzi matematyka. Zestawienie wymiarów dla konstrukcji narożnika przedstawia rys. 4.
LPKN=K*RPK
LPN=K*RP
LMN=K*RM
LDN=K*RD
Dla dalszej obróbki narożnika, tj. krycia deskami, płytą OSB, folią dachową jego przekrój powinien być pięciokątny (rys. 4, przekrój N1). Kąt ścięcia G obliczamy ze wzoru:
Przy wykonywaniu ścięć na narożniku pomocna jest wielkość ścięcia SG, wynosi ona SG = 1/2*BK*TAN G.
Ścięcie narożnika można wykonać pilarką tarczową lub stacjonarną wyposażoną w mechanizm pochylania piły.
Drugą trudność jaką sprawia cieślom więźba kopertowa jest wyznaczenie długości krokwi skróconych, tzw. kulawek – rys. 5. Łatwo udowodnić, że dla rozwiązania konstrukcyjnego koperty z rys. 3 długości kulawek dla połaci 1 wynoszą:
- dla pierwszej „kulawki”
LKk11 = LKD – (Rk1 – BK)/cos A – dS1 - dla drugiej i następnych
LKk1i = LKk11 – (i-1)*Rk1)/cos A
i – numer kolejny „kulawki”, a dla połaci 2:
LKk20 = LKD – dS2
LKk21 = LKk20 – (Rk2-BK/2)/cos A - dla „kulawek następnych
LKk2i = LKk21 – (Rk2*(i – 1))/cos A
gdzie i – kolejny numer kulawki licząc od kalenicy
dS1 i dS2 – skrócenie kulawek, wynikające z grubości krokwi narożnej
dS1 = dS2 = (√2 *BKN)/2*cos A
Przykładem odwróconego narożnika jest “kosz” czyli krokiew koszowa, która jest linią przenikania dwu połaci dachów dwupołaciowych, przecinających się pod kątem 90 stopni (tzw. elka) – rys. 6. Obliczenia dla kosza przyjmują tę samą postać co dla narożnika. Zestawienie wymiarów elementów dla takiego przypadku przedstawia wydruk z programu – tabela. Dokładność wykonania elementów więźby wynosi 3 – 5mm. Jest ona większa dla krokwi obrobionych struganiem. Rozstaw krokwi skróconych przy wykonaniu ich według obliczeń waha się w granicach 1 cm, maksymalnie do 2 przy mniej dokładnie wyciętym drewnie na tartaku (duży wpływ ma falistość powierzchni grzbietowej krokwi.
Niniejszy artykuł nie wyczerpuje wszystkich spotykanych przypadków konstrukcji ciesielskich, przedstawia tylko najprostsze. Do rozwiązania matematycznego zostały np.:
- dach kopertowy o pochyleniach połaci A1 i A2, lecz A1 ≠ A2 – przecięcie dachów dwupołaciowych pod kątem 90+Q
- stożki o podstawach wielokątów foremnych
- lukarny o wygiętych ściankach np. „wole oko”.
Rozwiązania matematyczne tych zagadnień postaram się przedstawić w następnych numerach.
| Inwestor | |||||
|---|---|---|---|---|---|
| Adres inwestycji | |||||
| Nazwa | cm lub stopnie | Nazwa | cm lub stopnie | ||
| 1 | Wys. Krokwi HK | 18 | Grub. Krokwi BK | 8 | |
| 2 | Wys. Krokwi HN | 22 | Grub. Narożn. BN | 14 | |
| 3 | Wys. Kosza HKO | 22 | Grub. Kosza Bko | 14 | |
| 4 | Wys. Płatwi HP | 22 | Grub. Płatwi BP | 14 | |
| 5 | Wys. Jętki HJ | 18 | Grub. Jetki BJ | 3,8 | |
| 6 | Wys. Pł. Kal. HPK | 14 | Grub. Pł. Kal. BPK | 14 | |
| 7 | Wys. Murłaty HM | 14 | Grub. Murłaty GM | 14 | |
| 8 | Wys. Sc. Kol. HKL | 62 | Poz. Podł. Piętra P1 | 284 | |
| 9 | Kąt Poch. Poł. 1 A1 | 40 | Kąt poch. Poł. 2 a2 | 40 | 10 |
| 10 | Kąt Ust. Nar. B1 | 45,00 | Kąt Ust. Nar. B2 | 45,00 | 52,898094 |
| 11 | Kąt Prz. Połaci GP1-2 | 54,07 | Wys. Na Podc. h1 | 18 | |
| 12 | Kąt Prz. Połaci GP1-3 | 62,97 | Kąt Ścięcia G1 | 27,03 | |
| 13 | Kąt Prz. Połaci GP2-3 | 62,97 | Kąt Ścięcia G2 | 27,03 | |
| 14 | Wys. Pom. HPM | 287,7 | Dług. Jętki LJ | 538,2 | |
| 15 | Skróc. Kulawki S1 | 12,9 | Skróc. Kulawki S2 | 12,9 | K2 |
| 16 | Krokwie 1 h2 | 18 | STAŁA K1 | 1,64441 | 1,64441 |
| 17 | Rozst. Kr. Kal. RPK1 | 7 | LPK1 | 9,1 | |
| 18 | Rozst. Płatwi RP1 | 200,0 | LP1 | 261,1 | RM1+RP1 |
| 19 | Rozst. Murłat RM1 | 500,0 | LM1 | 652,7 | 391,6 |
| 20 | Rozst. Dachu RD1 | 600,0 | LKO1 | 763,2 | 130,5 |
| 21 | KROKWIE 2 O1 | 100 | 1 | ||
| 22 | RPK 2 | 7,0 | LPK2 | 9,1 | |
| 23 | RP2 | 200,0 | LP2 | 261,1 | RM2-RM2 |
| 24 | RM2 | 500,0 | LM2 | 652,7 | 300,0 |
| 25 | RD2 | 600,0 | LD2 | 783,2 | 500,0 |
| 26 | NAROŻNIK O2 | 100,0 | LM2-1 | 652,7 | |
| 27 | LPKN | 11,5 | KAT Poch. Nar. AN | 30,682 | |
| 28 | LPN@ | 328,9 | Ścięcie SG1 | 3,57 | 3,5719152 |
| 29 | LMN | 822,2 | Ścięcie SG2 | 3,57 | 3,5719152 |
| 30 | LDN | 988,6 | DELTA HM2-1 | 0,0 | |
| 31 | LMN1 | 622,2 | Dług. Jętki LJ1 | 608,4 | |
| 32 | HPM1 | 258,3 | LJK1 | 397,1 | |
| 33 | Poprawka PG1 | 4,2 | Poprawka PG2 | 4,2 | 4,15333313 |
| 34 | RM2 rzecz. | 609 | Wysun. murłatO1-O2@ | 0,0 | 0,00 |
| 35 | A2 (obl.) | 34,55 | H Dachu | 513,5 | |
| 36 | Kąt krokiew-kosz | 37,45 | Kąt krokiew-kosz | 37,45 | 95,75555 |
| 37 | Odl. między krokw. OK1 | 80 | Odl. miedzy krokw. OK2 | 80 | |
| 38 | Liczba kulawek N1 | 7,60 | Liczba kulawek N2 | 7,50 | |
| 39 | Liczba kulawek N1c | 6 | Liczba kulawek N2c | 7 | |
| 40 | Długość kulawki LK11 | 676,3 | Długość kulawki LK21 | 770,3 | LK22-LK23 |
| 41 | LK12 | 571,9 | LK22 | 671,1 | 104,4 |
| 42 | LK13 | 467,5 | LK23 | 566,7 | |
| 43 | LK14 | 363,0 | LK24 | 462,2 | |
| 44 | LK15 | 258,6 | LK25 | 357,8 | |
| 45 | LK16 | 154,2 | LK26 | 253,4 | LK12-LK13 |
| 46 | LK17 | 0,0 | LK27 | 148,9 | 104,4 |
| 47 | Wys. krokwi nar.-kosz. | 23,8 | Wys. krokwi nar.-kosz. | 23,8 | |
| 48 | AN | 7,0 | BN | 7,0 | |
| 49 | Grubość deski podrynn. | 3,2 | Poprawka śc. Kr. Nar.2 | 0,00 | |
| 50 | Poprawka-skróc. Kr 2 | 0,00 | LKD-popraw. | 783,2 | |
| 51 | e 1-3 | 32,80 | S 1-3 | 32,73 | |
| 52 | e 2-3 | 32,80 | S 2-3 | 32,73 | |
mgr inż. Paweł Jatczak
ZUPH „Wiązar”
Usługi ciesielskie






Komentarze